Prečo pí?
Už v antike ľudia vedeli, že hodnota π je dôležitá, ale nemohli mať ani tušenia, ako veľmi významná bude. Dnes vedci a technici používajú π v širokej škále výpočtov týkajúcich sa kruhov a kriviek, od plánovania ciest alebo lietadiel až po analýzu zvukových vĺn. Keď obvod kruhu vydelíme jeho priemerom, dostaneme hodnotu pí.
Čo je pí?
Vieme, že hodnota π je približne 3,14. Presne túto hodnotu nemôžeme vyjadriť, pretože počet jeho desatinných miest je nekonečný a nenachádza sa v ňom žiadna perióda. Π sa nedá vyjadriť ako pomer dvoch celých čísel, takže hovoríme, že číslo π je iracionálne. Zároveň neexistuje žiadna nekomplikovaná rovnica, z ktorej by sa dala jeho hodnota vypočítať, preto ho nazývame aj transcendentným číslom. Toto všetko robí z π priam tajomné číslo.
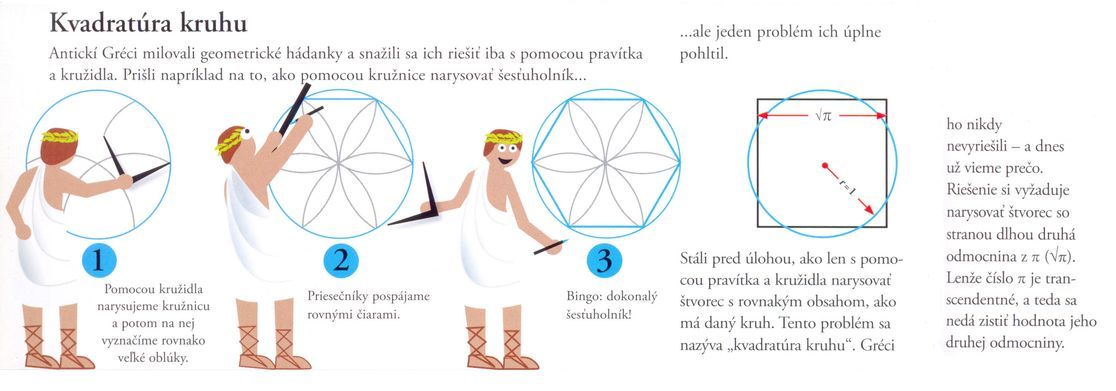
Kvadratúra kruhu
Antickí Gréci milovali geometrické hádanky a snažili sa ich riešiť iba s pomocou pravítka a kružidla. Prišli napríklad na to, ako pomocou kružnice narysovať šesťuholník…
…ale jeden problém ich úplne pohltil.
Stáli pred úlohou, ako len s pomocou pravítka a kružidla narysovať štvorec s rovnakým obsahom, ako má daný kruh. Tento problém sa nazýva „kvadratúra kruhu“. Gréci ho nikdy nevyriešili – a dnes už vieme prečo. Riešenie si vyžaduje narysovať štvorec so stranou dlhou druhá odmocnina z π. Lenže číslo pí je transcendentné, a teda sa nedá zistiť hodnota jeho druhej odmocniny.
Stavanie s kruhmi
Kruhy boli pre Grékov zaujímavé nielen v oblasti matematiky. Využívali ich pri stavbe polkruhových divadiel, pretože tak nielenže umožnili dobrý výhľad každému z divákov, ale zaoblený tvar aj zosilňoval zvuk. Grécke divadlá vyzerali pôsobivo a pritom mali jednoduchú konštrukciu. Stavali ich v prirodzene vytvorených jamách. Neskoršie civilizácie využívali kruhy pri budovaní tých najzaujímavejších stavieb na svete.
Hľadá sa pí
Fakt, že číslo π sa nedá presne vypočítať, nezastavil ľudí pred tým, aby to skúšali. Problém spočíval v odmeraní presnej dĺžky kružnice (zmeranie priemeru bola tá jednoduchšia časť). Skúšali to aj Egypťania. Narysovali si obrázok, ako je tu dole – kruh s vpísaným šesťuholníkom. Šesťuholník tvorí šesť rovnostranných trojuholníkov. Po obvode šesťuholníka je 6 strán týchto trojuholníkov a uhlopriečne sú 2.
Takže pomer obvodu šesťuholníka a jeho uhlopriečky (priemeru) je 3. Priemer kruhu tvoria 2 strany trojuholníkov a obvod je zjavne dlhší ako 6 strán, čiže hodnota π musí byť väčšia ako 3. Egypťanom sa podaril celkom slušný odhad hodnoty π ako pomer 162: 92, čo je 256:81, čiže 3,16.
Bližšie…
Okolo roku 250 p.n.l. grécky matematik Archimedes zistil presnejšiu hodnotu π pomocou vpísania kruhu medzi dva štvorce alebo iné útvary. Vďaka tomuto dômyselnému postupu sa viac priblížil k odmeraniu dĺžky obvodu kruhu. V prípade uvedenom tu musí byť napríklad obvod kruhu niekde medzi obvodmi dvoch nakreslených štvorcov. Archimedes prišiel na to, že k presnej odpovedi sa bude blížiť čoraz viac, ak bude zvyšovať počet strán tých dvoch útvarov.
…a bližšie
 Foto: Slovart
Foto: Slovart
Skúsil šesťuholník a výsledok sa spresnil. Čím viac strán pridával, tým viac sa strany útvarov približovali ku kružnici a jeho odpoveď sa spresňovala. Dopracoval sa až k útvaru s 96 stranami, ktorý už bol nerozoznateľne blízko pri kružnici.
Pomocou 96-uholníka zistil, že hodnota π je niekde medzi 3,1428 a 3, 1408 – úžasný úspech. Táto hodnota π bola najpresnejšou až dovtedy , kým ju o 500 rokov neskôr nespresnili čínski matematici…