Pôvabné trojuholníky
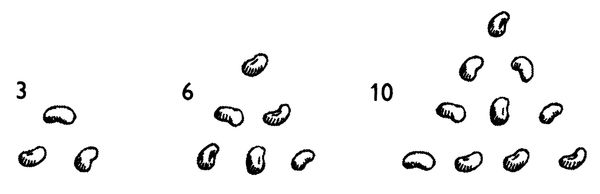
Väčšina Pytagorovej práce sa týkala trojuholníkov. Fascinovali ho trojuholníkové čísla, ako sú 3, 6 a 10, ktoré možno usporiadať do tvaru trojuholníka:
Pytagorova veta
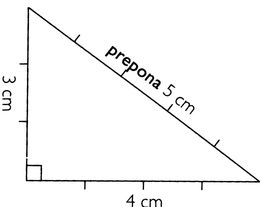
Pri Pytagorovom mene si väčšina ľudí spomenie na vetu o trojuholníku. Táto veta platí iba pre pravouhlý trojuholník. Podľa nej je súčet obsahov štvorcov, ktoré zostrojíte nad dvoma kratšími stranami – odvesnami -, rovný obsahu štvorca zostrojeného nad najdlhšou stranou – preponou. V tomto príklade majú strany dĺžky 3, 4 a 5 centimetrov. Obsahy štvorcov nad kratšími stranami sú 9 (3×3) a 16 (4×4). Výsledkom súčtu 9 a 16 je číslo 25. toto číslo je rovné súčinu 5×5, preto je prepona dlhá 5 centimetrov.
Pytagorova veta je praktická, pretože nám umožňuje určiť dĺžku jednej strany pravouhlého trojuholníka, ak poznáme dĺžky zvyšných dvoch strán. Existuje aj vzorec na jej výpočet : a2+b2=c2.
Bez fazule, prosím
Hoci veta nesie jeho meno, predpokladá sa, že sa o nej Pytagoras dozvedel v Egypte. Egypťania a Babylončania tento princíp využívali už stáročia. Existujú však pôsobivé teórie, ktoré pochádzajú priamo od Pytagora. Patrí medzi ne veda o zvuku, predstava o rotujúcej Zemi a názor, podľa ktorého „všetko je číslo“.
Pytagoras a jeho stúpenci boli takí tajnostkári, že o mnohých ich postupoch a myšlienkach nevieme. Historici vedia, že pytagorovci nejedli fazuľu, nesadali na misy určitých rozmerov a nedovolili lastovičkám stavať si hniezda pod ich strechami. Žiaľ, nikto netuší prečo.
Hrozivá dvojka
Je známe, že Pytagoras a jeho prívrženci milovali jednoduché veci, ktoré sa správali podľa pravidiel. Boli tiež presvedčení, že všetky čísla sa dajú vyjadriť ako jednoduché podiely – napríklad štvrtina je podiel 1 a 4, čo zapíšeme ako 1/4. Potom sa však objavilo čosi, čo ich vyviedlo z miery.
Ak pomocou Pytagorovej vety vypočítate dĺžku prepony trojuholníka, ktorého odvesny merajú 1 centimeter, stane sa čosi hrozivé.
Súčin 1 × 1má stále hodnotu 1. Keď tieto dva štvorce sčítate, dostanete obsah štvorca nad preponou: 2. Neexistuje jednoduchý spôsob zápisu čísla, ktoré po vynásobení samým sebou dá výsledok 2. Toto číslo poznáme ako druhú odmocninu z dvoch, alebo √2, ktorú nemožno zapísať ako podiel – je to nekonečné číslo, ktoré sa začína 1,414 2 a nikdy sa nekončí.
To pytagorovcov neuveriteľne dráždilo a tieto nekonečné, alebo iracionálne, čísla držali v tajnosti. Keď jeden z prívržencov, volal sa Hippasus, o nich neprestal rozprávať, zhodili ho z útesu a nechali utopiť sa!
Poverčivosť
Pytagorovci neboli jediní, čo neznášali určité čísla. Počas histórie priraďovali ľudia na celom svete rôznym číslam všelijaké významy. Napríklad v Číne sa číslo osem považovalo za veľmi šťastné. V iných krajinách to bolo číslo sedem. Niektorí ľudia verili, že číslo 13 prináša nešťastie. Existuje dokonca aj pomenovanie strachu z čísla 13 : triskaidekafóbia.
Aké záhadné!
Číselné hlavolamy známe ako magické štvorce sa zrejme prvý raz objavili v Číne. Niektorí ľudia po stáročia verili, že s ich pomocou môžu predpovedať budúcnosť. To je dosť nepravdepodobné, no predstavujú dobrý hlavolam!
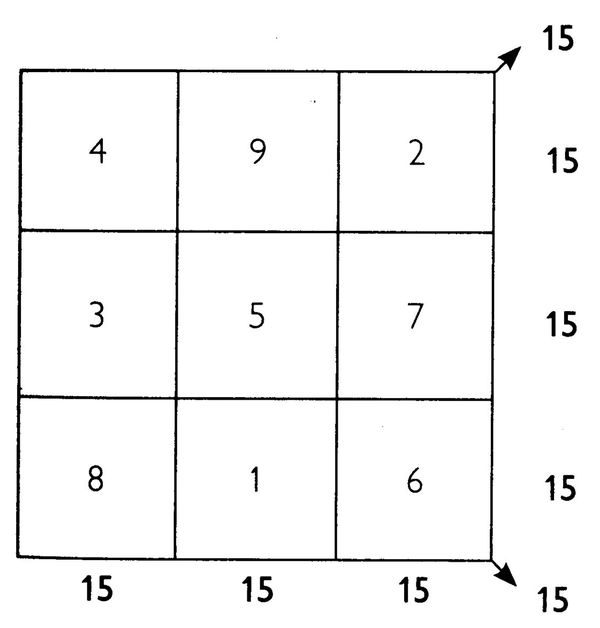
V magickom štvorci je súčet každého riadka, stĺpca a diagonály „konštantný“, čo znamená rovnaký. V tomto štvorci je súčet každého riadka, stĺpca a diagonály rovný číslu 15:
Rovným dielom
Predstav si, že máš dnes narodeniny a pozval si na čaj sedem priateľov. Ako rozrežeš koláč na osem rovnakých dielov tak, aby každý z vás dostal rovnakú porciu? Je to jednoduchšie, než sa zdá, ak vieš, čo máš robiť…
Pekné rezy
V matematike podiely označujeme pojmom zlomky. Ak sa chceš spravodlivo podeliť s koláčom so siedmimi ďalšími ľuďmi, musíš ho rozkrojiť na osem rovnakých častí. Inými slovami, každá porcia predstavuje jednu osminu koláča. Ako zlomok to môžeme zapísať 1/8. Horné číslo nazývame čitateľ a dolné menovateľ.
Krájame koláč
Pri krájaní koláča využiješ zlomky takto:
1. Najprv prekroj koláč na polovicu (1/2), aby si dostal dve rovnaké časti.
2. Každú časť znovu prekroj na polovicu. Takto dostaneš štyri rovnaké časti, pričom každá časť tvorí 1/4 koláča.
3. Nakoniec každú štvrtinu znovu prekroj na polovicu. Teraz budeš mať osem rovnakých kúskov. Každý kúsok predstavuje 1/8 koláča – dosť pre teba a sedem kamarátov, a celé sa to zaobíde bez hádok, kto dostal nespravodlivo viac!
Ťažkotonážne zlomky
Vo väčšine zlomkov je čitateľ menší než menovateľ. Tieto zlomky voláme pravé.
Niekedy sa však stretneš s menej obyčajným zlomkom, napríklad 11/2. Tento zlomok označujeme za nepravý, pretože jeho čitateľ je väčší ako menovateľ. Zlomok 11/2 je iba zápis pojmu 11 polovíc. Predstav si ako polovice koláčov – keby si ich spáril do celých koláčov, mal by si päť a pol koláča, čiže 51/2. Toto číslo voláme zmiešané, pretože je tvorené celým číslom a zlomkom.
Dokonalé percentá
Čo keby si musel rozdeliť koláč na nie na osem, ale na sto kúskov? Keby si potom chcel štvrť koláča, potreboval by si 25 rezov alebo 25/100. Toto číslo môžeme zapísať ako 25%, alebo %, čo znamená 25 zo 100 – v skutočnosti je 25% iba iný zápis pre 1/4.
Demaskovanie desatín Iný spôsob uvažovania o zlomkoch predstavuje výpočet podielu. V príklade s koláčom 1/4 znamená, že „rozdelíme koláč na štyri časti“. Ak do kalkulačky zadáš 1:4, výsledok bude 0,25. Toto číslo označujeme za desatinné číslo. Ak do kalkulačky zadáš 1:3, výsledok bude 0, 333 333 3… a trojky pôjdu do nekonečna. Nazývame ho periodické desatinné číslo. Aby sme ušetrili miesto, píšeme nad opakujúce sa číslice vodorovnú čiaru, takže 1/3 zapíšeme ako
A čo zaokrúhľovanie?
Niektoré čísla majú za desatinou čiarou veľa číslic. Napríklad číslo 0,4567 má štyri – nazývame to rozvoj na 4 desatinné miesta. Tieto čísla možno skrátiť „zaokrúhlením“ nahor alebo nadol. Ak chceš pracovať s dvoma desatinnými miestami, pozri sa na tretiu pozíciu – ak je rovná alebo väčšia než 5, ako je v prípade 0,4567, zaokrúhli číslo na 0,46. Ak je menšia než 5, ako napríklad číslo 0,6543, zaokrúhli číslo na 0,65.
Ťažké peniaze
Kedysi ľudia nepoužívali peniaze, ale navzájom si vymieňali tovar, napríklad dobytok. Takýto obchod sa nazýva barter. Povedzme si ale úprimne – dobytka sa do peňaženky veľa nezmestí, preto bolo treba nájsť alternatívu.
Ako prvé peniaze sa uplatnili prírodné predmety, ktoré boli pomerne vzácne a dostatočne malé na praktické nosenie – to mohlo byť čokoľvek od mušlí a ulít až po perie. Kovové mince sa začali používať okolo roku 700 pred n. l. v Lýdii, historickom území v Malej Ázii, a v Číne. Ak však ľudia chceli predávať či kupovať za veľké sumy, aj tak museli niesť veľký náklad mincí. V 12. storočí tento problém vyriešili v Číne vynájdením papierových peňazí.
Plastové peniaze
Tým sa však príbeh ani zďaleka nekončí. V súčasnosti je totiž väčšina peňazí uložená v počítačoch a elektronicky sa presúvajú medzi bankami, obchodmi a ľuďmi platiacimi kartami.
Úrok o rok
 Foto: Fortuna Libri
Foto: Fortuna Libri
Možno už máš v banke vlastný účet a tvoje úspory už zarábajú úrok. Ako však rozoznáš úrok od inflácie a čo to vlastne je?
Význam úroku je celkom jednoduchý. Vložíš peniaze na bankový účet a banka tieto peniaze používa. Za to ti vyplatí nejaké peniaze, ktoré sa nazývajú úrok. Ak si od banky požičiaš peniaze, naúčtuje ti za ne úrok ona. To znamená, že zaplatíš viac, než si si požičal.
Suma zarobeného alebo zaplateného úroku závisí od troch vecí – od množstva peňazí uložených v banke alebo požičaných od nej, od úrokovej sadzby banky a od času, na ktorý sú peniaze poskytnuté. Povedzme, že banka má pre úspory úrokovú sadzbu 10% za rok. Na účet vložíš 200€ a necháš ich tam rok. Po roku získaš 10% z 200€, čo je 20€ a o rok budeš mať na účte 220€.
Zhora nahor
Takmer všetko časom dražie. Infláciu, podobne ako úrok, vyjadrujeme v percentách – bežné rozpätie je 5% ročne. Preto ak dnes stojí čokoládová tyčinka 1€, môže o rok stáť 1,05€. Našťastie platy väčšinou rastú rovnakým tempom ako inflácia, takže držia krok so zdražovaním.